There are many different robotics drivetrains, one of the most common drive types that you will encounter is the Differential Drive. This control scheme is praised for its simplicity, ease of implementation, and ability to be used in many situations. This system is simply defined by two wheels independently controlled by their own motor.
Some examples of differential drive robots include, but are not limited to:
- Project LiftOff
- Edison
- iRobot Roomba
- e-puck
- Amazon Warehousing Robots (Kiva Systems)
In this article I want to bring a more nuanced understanding of this style of robot, discuss the kinematic model show how it is represented as a mathematical model, and pair this information with my robot kit to show how we can improve its performance with simple control systems. Let’s begin!
The Kinematic Model
Let’s establish our known constraints for a simple robot
Right away we know it has a pair of wheels that share an axis, these wheels are allowed to spin independently of each other either in the positive or negative direction of our choice. Each wheel will have the same radius, ![]() , and the distance between the wheels will be defined as,
, and the distance between the wheels will be defined as, ![]() .
.
![]()
D is the distance traveled (in the same units as d). ![]() is your speed in
is your speed in ![]() . Convert this as needed for your application. So if we assumed perfectly matched wheels and velocity we could use the above formula to determine distance traveled. Of course, life is not so easy on us.
. Convert this as needed for your application. So if we assumed perfectly matched wheels and velocity we could use the above formula to determine distance traveled. Of course, life is not so easy on us.
Intuitively, we understand that if both wheels spin with the exact same angular velocity, our system will move forward perfectly straight, and if perfectly opposed (negative and positive with the same magnitude) it will turn in place. Therefore, if we were to cause a difference between the angular velocity’s of the wheels ![]() or
or ![]() , we would get a corresponding change in the angular velocity of the system,
, we would get a corresponding change in the angular velocity of the system, ![]() , hence we will see our robot make a curved path. Now, you can visualize this just like when you draw a circle or arc with a compass, the marking end is the robots’ path and the anchor is where the center of the curve is. This anchor point is known as the Instantaneous Center of Curvature (I.C.C). This isn’t going to be useful to us if we can’t control this behavior or predict where our robot is going to go, we need some equations and feedback to assist us.
, hence we will see our robot make a curved path. Now, you can visualize this just like when you draw a circle or arc with a compass, the marking end is the robots’ path and the anchor is where the center of the curve is. This anchor point is known as the Instantaneous Center of Curvature (I.C.C). This isn’t going to be useful to us if we can’t control this behavior or predict where our robot is going to go, we need some equations and feedback to assist us.
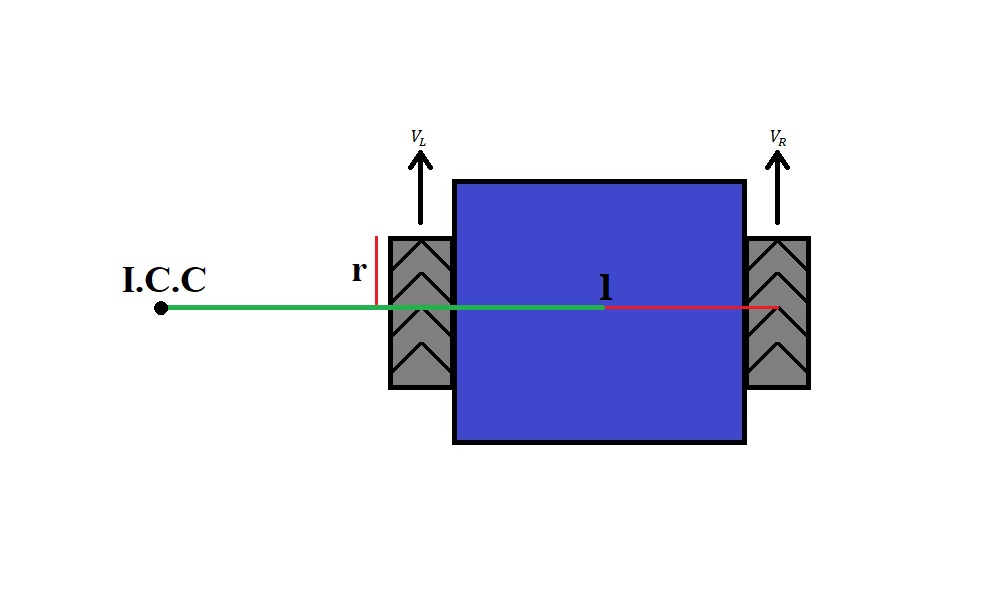
Kinematics
Odometry
In simple terms, Odometry is the use of sensors to track the location of the robot.
